jueves, 30 de agosto de 2018
SOLUCIÓN DE ECUACIONES TRIGONOMÉTRICAS
Una ecuación que contiene funciones trigonométricas es llamada una ecuación trigonométrica .
Ejemplo:
Una ecuación trigonométrica es una ecuación que contiene una o varias funciones trigonométricas de la variable trigonométrica del arco x. Despejar “x” significa encontrar los valores de los arcos trigonométricos, cuyas funciones trigonométricas hacen que la ecuación trigonométrica sea correcta.
Las respuestas, o valores de los arcos de solución, se expresan en grados o radianes. Ejemplos:
x = Pi/3; x = 5Pi/6; x = 3Pi/2; x = 45⁰; x = 37,12⁰; x = 178,37⁰
Conoce el concepto de resolución.
- Para resolver una ecuación trigonométrica, transfórmala en una o en varias ecuaciones trigonométricas básicas. Finalmente, la resolución de ecuaciones trigonométricas da como resultado la resolución de 4 tipos de ecuaciones trigonométricas básicas.
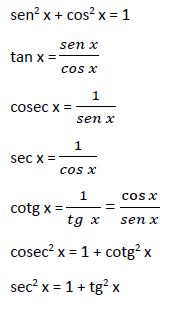
Conoce cómo resolver ecuaciones trigonométricas básicas.
- Existen 4 tipos de ecuaciones trigonométricas básicas:
- sen x = a ; cos x = a
- tg x = a ; cotg x = a
- Resolución de los procedimientos de las ecuaciones trigonométricas básicas mediante el estudio de distintas posiciones del arco x en la circunferencia unitaria y mediante el uso de la tabla de conversión trigonométrica o calculadora. Para saber completamente cómo resolver estas ecuaciones trigonométricas básicas y similares, lee el libro titulado: "Trigonometry: Solving trig equations and inequalities" ("Trigonometría: Resolución de ecuaciones y desigualdades trigonométricas") (Amazon E-book 2010).
- Ejemplo 1: resuelve sen x = 0,866. La tabla de conversión o calculadora te da x = Pi/3 como respuesta. La circunferencia unitaria da otro arco (2Pi/3) que tiene el mismo valor del seno (0,866). Además, la circunferencia unitaria da una infinidad de respuestas que se denominan soluciones extendidas.
- x1 = Pi/3 + 2k.Pi, y x2 = 2Pi/3 (soluciones en el intervalo (0, 2Pi))
- x1 = Pi/3 + 2k Pi, y x2 = 2Pi/3 + 2k Pi (soluciones extendidas)
*Las relaciones trigonométricas también pueden ser consideradas como funciones de una variable que es la medida de un ángulo.
Esta medida de ángulo puede ser dada en grados o radianes . Aquí, usaremos radianes. Ya que cualquier ángulo con una medida mayor que 2 π radianes o menor que 0 es equivalente a algún ángulo con medida 0 ≤ θ < 2 π , todas las funciones trigonométricas son periódicas .
La gráfica de la función seno se ve así:
Dese cuenta que el dominio de la función y = sin x es todos los números reales (el seno está definido para cualquier medida de ángulo), el rango es −1 ≤ y ≤ 1.
La gráfica de la función coseno se ve así:
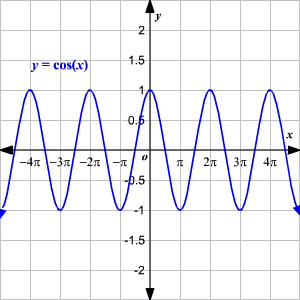
El dominio de la función y = cos x es todos los números reales (el coseno está definido para cualquier medida de ángulo), el rango es −1 ≤y ≤ 1.
El dominio de la función y = tan x es todos los números reales except o los valores donde el cos x es igual a 0, esto es, los valores 
para todos los enteros n . El rango de la función tangente es todos los números reales.
para todos los enteros n . El rango de la función tangente es todos los números reales.
La gráfica de la función secante se ve así:
El dominio de la función 
es otra vez todos los números reales excepto los valores donde el cos x es igual a 0, esto es, los valores para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
es otra vez todos los números reales excepto los valores donde el cos x es igual a 0, esto es, los valores para todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
La gráfica de la función cosecante se ve así:
El dominio de la función 
es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πnpara todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πnpara todos los enteros n . El rango de la función es y ≤ −1 o y ≥ 1.
La gráfica de la función cotangente se ve así:
El dominio de la función 
es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πnpara todos los enteros n . El rango de la función es todos los números reales.
es todos los números reales excepto los valores donde el sin x es igual a 0, esto es, los valores πnpara todos los enteros n . El rango de la función es todos los números reales.
TOMADO DE :
https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/trigonometric-functions
https://www.aulafacil.com/cursos/matematicas-secundaria-eso/ecuaciones/resolucion-de-ecuaciones-trigonometricas-l29550
https://es.wikihow.com/resolver-ecuaciones-trigonom%C3%A9tricas
Suscribirse a:
Entradas (Atom)